10月 13th, 2016 Posted 12:00 AM

規というのはコンパスを意味していると聞いています。
ぶん回し、あるいは円規は定規に対した言い方です。
おそらく、小学生のころにこのぶん回しと出会いました。
それは、時計を覚えるために算数のノートに、
時計を書き込むことか、円グラフを描くための文房具としてです。
実際、これも自分のコレクションです。
様々なコンパスを持っていますが、実はこの写真のコンパスを
一時、どこかに忘れていて2年ほど、正直困っていたのです。
このコンパスは、プロのデザイナーになって直ぐに手に入れたモノです。
それだけに、歳末にはこのコンパスをきれいにしていました。
最近、図面などはパソコン上で簡単に描いてしまうことができますが、
たとえば、五角形はコンパスで描くことの手続きなどは、
コンパスの使いごこちを確かめる重大な手法だと思っています。
最近のプロのデザイナーには、無意味なモノになろうとしていますが、
自分はあえて、製図機器の重大なモノは、コレクションの一つです。
あらためて「規」という文字は、取り決めやルールのことであり、
円規というのは中心点との距離を保ったままに円形を描くことです。
したがって、コンパスという意味を見直す意味でも、
文房具、製図機器としてのモノの意味は見直すべきでしょう。
* 5月25日Staff Blog
* 「光造形は日本で発明されて、今やナノテク世界で進化している」
* 『工業デザイン教育での「手」のトレーニング』
* 「デザイン解としての回答、その強度」
* 『研究室のMac環境は最高性能の自分デザイン』
Tags: CAD, コレクション, コンパス, パソコン, ぶん回し, 中心点, 五角形, 使いごこち, 円グラフ, 円規, 図面, 定規, 文房具, 時計, 算数, 製図機器, 規
Posted in ConsilienceDesign, 企望を「までい」具現へ, 祈望から企望へ
目次を見る
3月 9th, 2010 Posted 12:01 AM
結果判断という課題
結果判断から考えを深めていくには、
その結果を様々な観点からとらえ直さなければなりません。
結果をまず問題としてみるなら、
いくつかの「考察」方法が必要です。
問題というのも、結果に対する意識の中では、
話題・課題・問題という分別が必要です。
そして、話題ならばそれは思いつきで答えればいいのです。
回答
ところが、課題となると、「回答」を求めることになります。
その「回答」というのは、「回」という文字形態が示すように、
二重構造を持っています。
課題=Questionに対する回答=Answerです。
したがってすでに課題には、
自分の知る・知らないにかかわらず、一般解がある!と
考えて構わないでしょう。
それは、思考方法を「学」として学んできた算数や数学は、
常に、問題=課題に対しては、
回答に至る手続きを知る、あるいは暗記しておけば、
必ず、「答え」にたどり着くわけです。
�二重構造の強さ
私が、二重構造というのは「回答」の世界観です。
デザイン教育では、まず「課題」を与えて、
デザイン回答をやらせます。
それは、デザイン思考のトレーニングとして、
このデザイン解では、あれが足らないとか、
機能性を果たしていないとか、さらに問題が発生する、
という訓練です。
つまり、「回答」として提示されたデザイン解には、
二重性があるという見抜き方が必要です。
二重性には、性能的には「強度」があります。
すなわち、デザインは「綺麗事」だというある意味では、
開き直りの強さこそ、「回答」としてのデザイン解、
その強さだとひとまず考えておきたいと思います。
Tags: Answer, Question, デザイン思考, デザイン教育, デザイン解, トレーニング, 一般解, 世界観, 二重構造, �二重構造の強さ, 問題, 回答, 強度, 思いつき, 数学, 方法, 暗記, 機能性, 答え, 算数, 結果判断, 綺麗事, 考察, 見抜き方, 観点, 訓練, 話題, 課題, 資本主義からの闘争
Posted in 016「デザインと答」, 資本主義から逃走せよ!
目次を見る
1月 16th, 2010 Posted 9:00 AM
美しい
私は「生まれ変わってもデザイナーになりたい」です。
なぜなら、
まず、自分の中に「美しい」と自身で確認できる、
そんなモノやコトがひそんでいるのかを知りたいから。
そして、「美しい」というのは何なんだろうと
いつも問いかけていたいからです。
しかもどん欲に、「これって美しい」でしょ!
見せびらかしたいのです。
デザインは結局「造形」に集約させることができます。
そのための思考・思って、考える、ということは、
「数理的だ」と想ってきました。
「数学的」っていうのは受験の思い出が重なって、
「間違ってはいけない」というストレスがトラウマ。
数理
しかし、「数理」というのは、
たとえば、「リンゴ1個」と「鉛筆1本」を
総和して想う=思い考えるとすると、
●「思って」、たとえば二つとも「赤い」とか、
●「考えて」、「丸い」と「細い」ということです。
だから、数学・算数だと1+1=2となって
総和で「2」だけしか残りませんから、
何の感動もありません。
だから、
●「リンゴの赤さ」と「細い棒の中に黒い芯」を
たとえば、
●「リンゴに突き刺してもそれで絵が描ける」となると、
「どういうこと?」
「なぜ?」
「それがどうしたの?」っていう疑問が沸いてきて、
これはまぎれもなく「リンゴ鉛筆」の「造形」です。
想・思・考=形
「数理的」というのは、実はこうした想像力で、
●とんでもなく、「食べられる鉛筆」になったり、
●「鉛筆でリンゴにいっぱい穴を開けるモノ」
にもなってしまうのです。
私が「デザイン数理学」ってむずかしく言っている、
● e・i・πなんて「記号」の組み合わせは、
e=鉛筆・i=芯・π=リンゴがマイナス1って何?
これらを組み合わせることを想像力=virtualで、
「想う」=「思う」と「考える」ことをすると
「形」が出来ている、という「造形」です。
めいっぱい「オイラーの想像力」を追いかけて、
「見えてくるコト、ひょっとするとつかめるモノ」が
「美しさ」になっているのかも・・・ということです。
数学的美しさ・数理的美しさ
だから、「数学的美しさ」と「数理的美しさ」が、
同一なのか、全く異なっているのかは、私はもちろん、
人類はまだ分かっていないということにもなります。
Tags: 「資本主義からの逃走」, e, i, Virtual, π, オイラーの想像力, コト, ストレス, デザイナー, デザイン, デザイン数理学, モノ, リンゴの赤さ, リンゴ鉛筆, 受験, 形, 思, 思い出, 思う, 思考, 想, 想う, 想像力, 感動, 数学, 数学的, 数理, 数理的, 算数, 組み合わせ, 総和, 美しい, 考, 考える, 見せびらかし, 記号, 造形, 集約, 食べられる鉛筆
Posted in 900「かたちと造形思考」, 資本主義から逃走せよ!
目次を見る
12月 1st, 2009 Posted 7:39 PM
「デザイン」は、「問題解決の方法」だとこれまで、
ズッーと私は、一般に、学生に、企業に伝えてきました。

それも「問題解決」でありしかも「難問解決」なのです。
その唯一の方法だとさえ確信しています。
ただし、宗教ではありません。奇跡は起こせません。
まして、科学・技術・芸術でもないのです。
科学と技術とを接着・融合させるたった一つの方法です。
ところで「科学技術」という日本語は大きな間違いです。
哲学者・中村雄二郎先生は、
「科学」は「分科学」の略語にすぎないと教えられました。
デザインの難問解決という論議から、
問題解決の簡潔な方程式を、
私はデザイン思考の基本と基準にしてきました。
つまり「問題」には、
●「話題」=Topics
●「課題」=Question
●「問題」=Problem
があります。
この解決は、
■ Topics – Reply
■ Question – Answer
■ Problem – Solution
ということまでが、本来の方程式=equationです。
この方程式は、デザインでは次の二つになります。
AlgorithmとProgramです。
そこで、「資本論」のために、
マルクス(数学に関する遺稿集)が、なぜ導関数を
エンゲルスに教えたのかがわかるはずです。
数学的思考は、応答と回答は、
「算数」や「数学」で学ぶことができます。
芸術も、応答的な作品と回答的な作品しかありません。
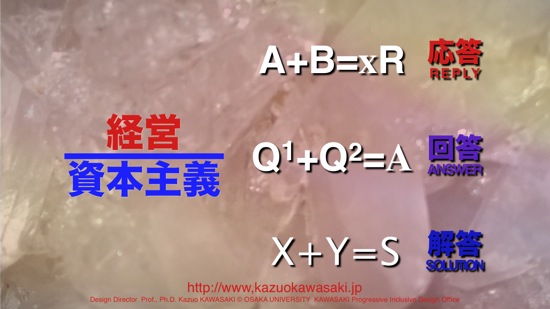
本来、「問題解決」・「難問解決」によって「解答」が
創出されるのです。
創出されるから、クリエィティブでなければいけません。
しかも「解答」は美しさが必要です。
私は、「逃走する方程式」はかくあるべきと考えています。
そして、デザインには、
「デザイン数理学」というAlgorithmとProgramが、
「分科学」として「技術」を支え、
造形言語によって美しさが創出されるのだと思います。
「資本主義から逃走できるデザイン」、
その時代を牽引できるデザイナーは限られているのは、
多分、「仕分けられた」才能でしょう。
Tags: 「資本主義からの逃走」, Algorithm, Answer, equation, Program, Question, Reply, Solution, Topics, エンゲルス, クリエィティブ, デザイン, デザイン数理学, マルクス, 中村雄二郎, 企業, 作品, 分科学, 創出, 問題, 問題解決, 奇跡, 学生, 宗教, 導関数, 応答, 才能, 技術, 接着, 数学, 数学に関する遺稿集, 数学的思考, 方法, 方程式, 時代, 牽引, 科学, 算数, 美しさ, 芸術, 融合, 話題, 課題, 資本主義から逃走できるデザイン, 資本論, 逃走する方程式, 造形言語, 難問解決
Posted in 007「資本主義」, 資本主義から逃走せよ!
目次を見る



