6月 15th, 2016 Posted 12:00 AM

「Scientist」という呼称を造ったWilliam Whewellについて知りたい、
このことを追いかけてきました。
ウィリアム・ヒューエルの専門はMineralogy=鉱物学でした。
当時の鉱物学は現代の鉱山学とは違っていました。
鉱物学は、現代では地球物理学に等しく、数学・物理学はもちろん、
哲学にまで及ぶ科学全般までの学問・学域だったようです。
したがって、Physician もCatastrophism、そしてConsilienceの造語にまで
見事に科学全般の統合性を訴求していたことは当然でした。
そして、本来は分科学であったことから、
科学は、その分化とともに専門性に深度を持つようになってしまいました。
彼の造語が今あらためて脚光をあびるようになったのは、
分科学ではなくて科学性の統合こそ、実は科学の本質であるとした
エドワード・オズボーンによるものでした。
彼の専門は自然学であり、
彼は社会自然学にコンシリエンスを採用しました。
社会自然学の統合性は保健学=Health Scienceで再度取り上げられ、
自分がデザインを加味したのも、デザイン科学としたときには、
科学の文科系と理科系、さらに学術性と芸術性の統合が必要ということを
デザインとして、その進化には最もふさわしいという発想からでした。
コンシリエンスデザインという統合性には、
● 規模的統合
● 機能的統合
● ネットワーク的統合
● 文化的統合
この四つの統合性からは、
いわゆる「コンセプト発想」は消滅していきます。
コンシリエンスデザインは確実にコンセプト発想では、
大きな間違いが含まれることを
これからは証左していくことになるでしょう。
*『統一、いや統合には四つの分類があるが気づくだろうか』
*『silience=無意識だけれども重要な知的核心という解釈』
*『これからのデザインを語るために=・・・signare・・・』
*『コンシリエンスデザイン学域の統合図解』
*『『学際化』によって危機管理デザイン工学をめざす』
Tags: Catastrophism, Consilience, Health Science, Mineralogy, Physician, Scientist, William Whewell, ウィリアム・ヒューエル, エドワード・オズボーン, コンシリエンス, コンシリエンスデザイン, コンセプト, コンセプト発想, デザイン, デザイン科学, ネットワーク的統合, ふさわしい, 保健学, 全般, 再度, 分化, 分科学, 加味, 呼称, 哲学, 地球物理学, 学問, 学域, 学術性, 専門, 専門性, 当時, 当然, 必要, 採用, 数学, 文化的統合, 文科系, 本来, 本質, 機能的統合, 消滅, 深度, 物理学, 現代, 理科系, 発想, 確実, 社会自然学, 科学, 科学全般, 科学性, 統合, 統合性, 脚光, 自然学, 芸術性, 見事, 規模的統合, 訴求, 証左, 造語, 進化, 鉱山学, 鉱物学, 間違い
Posted in ConsilienceDesign, 企望を「までい」具現へ, 危機解決をめざすデザイン実務
目次を見る
6月 23rd, 2014 Posted 12:12 AM

デザイナーが、数学「的」な見解を述べようものなら、
知ったかぶりした数学「屋」に限って能なしの輩をみかけます。
したがって、本来の数学的な仮説である「ひも理論」以前に、
これも私の趣味であり、私が使い慣れている紐やロープについて
書いておこう思った次第です。
おそらくヨットに長けた人ならばロープの使い方は熟知しています。
私は、父から逮捕術での紐やロープ使いを幼児の頃から教わり、
高校の山岳部時代にはロープ使いを訓練させられました。
私の得意技に紐使い、ロープ使いがあります。
そして、それこそ数学の仮説である「超ヒモ理論」を教養として、
私なりにそれをデザインへの応用を考えてきました。
最も、数学屋が紐やロープ使いはできるはずがないでしょう。
たった一本の紐、とりわけ、その結び方やその展開方法は、
何か、趣味がなければ学校では教えていません。
夜の星・星座名や道端の草花名を教えないことに等しいのです。
本来、小学校時代に恐竜を教えたり、草花、高山植物、天気図など
絶対に教えるべきだと私は思っています。
結局日教組の先生が日本の教育を壊してしまったと確信しています。
その最大の理由は、
今、紐やロープを手法として教えられるでしょうか?
たとえロープ使いは難しいかもしれませんが、紐程度の扱いは、
トレーニングとして教え込むべきだと思っています。
大学人になって紐・ロープを扱える人間に会ったことがありません。
それこそ、数学屋で「ひも理論」を語ることができても、
金槌の使い方も知らないのに、建築を語ろうとするようなものです。
以前、高名な建築家をある有名な評論家が「彼は釘も打てない」と。
「君はそんな人物になってはいけない」と諭されました。
時折、手元にある「紐」と戯れるとき、
私はいつもこの一流の批評家の話を思いだします。
『最も嫌いだった著作からこれを始めた』
Tags: 「ひも理論」, 「超ヒモ理論」, デザインへの応用, ヨット, 天気図, 山岳部時代, 建築家, 数学, 日教組, 紐やロープ, 結び方, 草花名, 金槌の使い方, 釘も打てない, 高山植物
Posted in 企望を「までい」具現へ, 危機解決をめざすデザイン実務, 祈望から企望へ
目次を見る
5月 22nd, 2013 Posted 12:00 AM

これは厳密にはいわゆる数学でのクラインボトルではありません。
しかし、3Dの造形においては、
「造形システム」での手法や装置が極めて重要です。
たとえば、
なぜ、Desk Top Publishing=DTPが時代要請だったのだろうか?
この質問に戻らなければなりません。
DTPではPostScriptというOSが無償でユーザーに供給されました。
結果、PageMakerというレイアウトソフトは1986年に生まれ、
Illustrator88がその期待の元に出てきました。
世の中はレーザープリンターの印刷精度値を進化させるのです。
商店街から「軽印刷業」が消滅を始めました。
これは2Dの「版」離れを意図した世界観的な存在感、
少なからずパソコン自動製版と呼ばれた革新でした。
同時期に日本では光造形という実験成果で特許を求めましたが、
見送られた現実がありました。
2Dの世界観を3Dに求め始めるのは当然でした。
その一人がデザイナーの私だったのかもしれません。
明確にニュージャージーのベンチャーとプリンストン大学が、
「歯車」をすでに実現していました。
私は、この装置が欲しく、3D-CGと3D-CADを学ぶために
ベンチャーの本社(トロント)で二夏訓練を受けました。
3D-CGでは、Natural Phenomenaという
今では当たり前の、水と水飛沫や燃える火、夕焼け表現でした。
しかし、私の頭の中では、金型=「型」から解放される、
そんなモノづくりを夢見ていました。
光造形のクラインボトルは、
「何のため?」とどれだけこれまで聞かれたことでしょうか?
想像力のある人は、
金型では決して出来ない自由な表現や実務対象を見つけました。
そこで現代では拳銃やマシンガンさえ3Dプリンターでの
実現可能性が明確になり始めてしまいました。
わが国、日本の技術進化=「技」の系譜は、
はっきりと光造形の下敷きの上に、
3Dプリンターの「技」が確かめられることが分かりました。
このクラインボトルの形態を自由に変形させ、
かつ様々なイメージをそのまま造形化するのに、
廉価な3Dプリンターでもここまで出来ること、
これが重要だということです。
Tags: 1986年, 2D, 3D, 3D-CAD, 3D-CG, 3Dプリンター, DTP, Illustrator88, Natural Phenomena, OS, PageMaker, PostScript, イメージ, クラインボトル, デザイナー, トロント, ニュージャージー, パソコン自動製版, プリンストン大学, ベンチャー, マシンガン, ユーザー, レーザープリンター, レイアウトソフト, 下敷き, 世界観, 光造形, 印刷精度値, 商店街, 型, 変形, 夕焼け, 夢, 実務対象, 実現可能性, 実験成果, 廉価, 形態, 想像力, 手法, 技, 技術進化, 拳銃, 数学, 日本, 時代要請, 歯車, 水, 水飛沫, 消滅, 無償, 燃える火, 版, 特許, 現代, 現実, 系譜, 自由, 表現, 装置, 解放, 軽印刷業, 造形, 造形システム, 進化, 金型, 革新, 頭の中
Posted in 企望を「までい」具現へ, 危機解決をめざすデザイン実務, 祈望から企望へ
目次を見る
4月 27th, 2013 Posted 12:00 AM
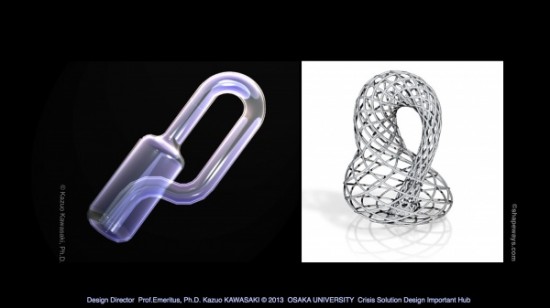
光造形システムでこれが可能だろうか、
という私の直観は、フィラデルフィア大学の
Eminent Scholarと呼ばれていた元医学部の名誉教授たちの質問でした。
確かに、トポロジー、日本では「位相空間」という数学思考の形態でした。
私はトポロジーを位相空間と翻訳する大間違いに気づきました。
以後、私は空間は元来、形態であり言語だと考えてきました。
つまり、
・点には形が無い
・線には太さが無い
・面には厚さが無い
これらが数学的な想像力で、
場の近傍性=トポロジーということになりました。
ところが、
あるアーティスト(「点・線・面」の著者/カンディンスキー)が、
「点とは必ずこれは正方形になるといづれ理解される」。
この予測に心を惹かれました。
・点はピクセルを単位とする
・線はピクセル設定で太さが出来る
・面は、そうした線の太さで厚さが生まれる
このことを、当時のIDEAS(3D-CAD)でSLAデータにしましたが、
「クラインボトル」には厚みがあっても、サポーター設定が困難でした。
しかし、サポーター設計が光造形の決め手になることで、
確実に厚さがある「クラインボトル」=擬似形態が出来ました。
それから光造形形態を「トポロジー空間」と呼ぶことで、
3Dプリンターはサポーター無しで、
いわゆるレイヤー=面を積層することで、
言語→形態→空間設定がいわゆる編み目表現を可能にしました。
したがって、あくまでも見た印象は「クラインボトル」でも、
光造形と3Dプリンターはまったく異なります。
ただし、この編み目そのものが管=パイプになったとき、
それはトポロジーという数学的思考は、
デザイン的思考となり、素材がパイプになれば、
それこそ、トポロジー空間論は完成するでしょう。
Tags: 3D-CAD, Eminent Scholar, IDEAS, SLAデータ, アーティスト, クラインボトル, サポーター, トポロジー, パイプデザイン的思考, ピクセル, フィラデルフィア大学, レイヤー, 位相空間, 光造形システム, 厚さ, 名誉教授, 太さ, 形, 形態, 想像力, 数学, 数学思考, 日本, 正方形, 点, 線, 翻訳, 言語, 面
Posted in 企望を「までい」具現へ, 危機解決をめざすデザイン実務, 祈望から企望へ
目次を見る
1月 24th, 2013 Posted 12:00 AM

「機能的なことがデザイン」とか、
「機能美の追求がデザイン」とよく言われます。
40年デザイナーでいる私の結論は、
機能とデザインの関係は、
デザインの本質の一部でしかないということです。
グッドデザインに関する「祝祭のあとに」という私の論文*で、
「性能・機能・効能」の構造論を述べていますが、
端的に表現すると、基本図形である「三角形」を事例にすれば、
三角形には、図形でしかないにも関わらず、
三角形には様々な「性質」が備わっています。
三点が三辺で結びつけられているだけの「かたち」ですが、
この「かたち」をシンボルにするだけで、様々な意味を与えたり、
意味されていることが人類はいっぱい蓄積してきました。
最も論理的に三角形の「性質」は、
数学や幾何学で、公理としてまとめられています。
それらは数学・幾何学に任せておき、
その性質を運用することで、
三角形の「性能」を産み出すことが可能です。
私は、特に、丸・三角・四角を自分の造形要素として
徹底的に利用してきました。
だから、ブルーノ・ムナーリは、丸・三角・四角、
それぞれの性質をデザイン、あるいは造形として語っていますが、
私なりの図形の「性質」から「性能」を書き残そうと考えています。
それは、三角形を描くだけで、
「発想」をより強化する手法があるということです。
これまで、大学では勿論ですが、
企業研修での「発想法」として紹介してきました。
今、流行しているマインド・マップは
私は全くつまらない発想法だと思っています。
むしろ、図形、丸・三角・四角という「かたち」に「ことば」を乗せれば、
それが、丸・三角・四角の「性質」を
視覚的にシンボルとして認識することが可能です。
このシンボル化がそのまま「性能」を持つということになります。
そして、この「性能」あるシンボルが、
何らかの働きや刺激を与えることが「機能」です。
そして、性能が機能を果たすことで、
「効能」という社会的な存在意味が生まれてくるということです。
ちなみに、三角形を配置するパターンはいくつあるでしょうか?
ずばり、四種類です。
ということは、「三角形には基本的に4つの性能がある」ということです。
*
「2003年度グットデザイン賞 審査総評
After Celebration – What as Demonstration is a Good Design
祝祭のあとにー論証としての何がグットデザインであるのか」
(『グットデザインアワード・イヤーブック GOOD DESIGN 2003 2004』、
日本産業デザイン振興会、2004年1月、4-9 ページ)
Tags: 40年, かたち, グッドデザイン, ことば, シンボル, デザイナー, ブルーノ・ムナーリ, マインド・マップ, 三点, 三角, 三角形, 三辺, 丸, 人類, 企業研修, 効能, 四種類, 四角, 図形, 大学, 幾何学, 性能, 性質, 意味, 手法, 数学, 機能, 機能的なことがデザイン, 発想, 発想法, 論文, 造形要素
Posted in 企望を「までい」具現へ, 祈望から企望へ
目次を見る
10月 20th, 2012 Posted 3:34 PM
目次を見る
9月 18th, 2012 Posted 1:35 PM
9月18日 壬午(仏滅)
数学的には、点には大きさがない、
よって、もちろん「形体」もない。
付け加えるならば、
「点という形体」
は数学的根拠であり、
「形体としての点」は、
芸術的根拠とことわり書きを
付け加えておくべきだろう。
倉俣史朗のデザイン『夢の形見に』11 造形元素としての点
目次を見る
10月 11th, 2010 Posted 12:00 AM
数「学」と物「理」
美大系へ進学するのは、特殊な「ひと」。
今もそのいわば常識のようなことが蔓延しているようです。
私も出身高校に、浪人後、美大に合格したと報告に行ったとき、
職員室で、どよめきがありました。
「ウソだろう、なぜなんだ、なんで美大なんだ」と言われました。
その反響に私自身が驚いたほどです。
問題は、数学とか物理というのは、「理系」であり、
「理系」と「文系」、この種別を日本の高校で決定しようという制度になっていることでしょう。
無論、職能として「数学者」や「物理学者」、
いやもう少し広範囲に「数学系学者」と「物理系学者」にとって、
それぞれの「専門」としての数学と物理は、先端系=未知探索へ向かっています。
さて、それならデザインにとって、
数学と物理がどこかでしかも無意識的かもしれないほど介在している概念があるかもしれません。
私は、数学の「学」と物理の「理」、つまり、学と理に注目してきました。
焦点連鎖の「次元」
結果、数学的に焦点化していることと、物理的に焦点化していること、
それはそれぞれの差異が明確である概念として、「次元」がその焦点だ、とみてきました。
次元=dimensionです。これもいづれ「デザイナーとして」整理します。
このことに気づいたのは、
EWSというコンピューターと出逢った時からの印象的な、私なりの一つの結論です。
デザイナーは「かたち」=形態を造形化する職能です。
ただし、デザインもすでに「デザイン系」と言うほど拡大と拡張をしています。
かって、インダストリアルデザインが「口紅から機関車まで」と言われました。
私は、「日本酒から人工臓器」とか、「タワシから原子力」など、
様々なフレーズで、デザイン系の広がりをあえてアジテーションしてきました。
こうしたフレーズの中でデザイン対象となる形態・空間に、私は「次元」を置いています。
その理由は、数学的次元と物理的次元の差異性・同等性には、
基本的な思考軸が「学」であり「理」だと思うからです。
学際化の超「次元」
そしてこの「学理」の学際化にこそ、
デザインが寄与する役割は「空間・形態・次元」の連鎖系にあるものと推察しています。
ところがデザイン以上に、
現代アートは先んじて、いとも簡単に超「次元」的、主観的な連鎖表現をしています。
Tags: dimension, インダストリアルデザイン, かたち, タワシから原子力, 先端系, 口紅から機関車まで, 学, 学理, 学際化, 常識, 形態を造形化, 数学, 数学系学者, 数学者, 文系, 日本酒から人工臓器, 未知探索, 次元, 物理, 物理学者, 物理系学者, 理, 理系, 空間・形態・次元, 美大系, 連鎖系, 連鎖表現
Posted in 054「多次元性への造形思考」, 資本主義から逃走せよ!
目次を見る
3月 9th, 2010 Posted 12:01 AM
結果判断という課題
結果判断から考えを深めていくには、
その結果を様々な観点からとらえ直さなければなりません。
結果をまず問題としてみるなら、
いくつかの「考察」方法が必要です。
問題というのも、結果に対する意識の中では、
話題・課題・問題という分別が必要です。
そして、話題ならばそれは思いつきで答えればいいのです。
回答
ところが、課題となると、「回答」を求めることになります。
その「回答」というのは、「回」という文字形態が示すように、
二重構造を持っています。
課題=Questionに対する回答=Answerです。
したがってすでに課題には、
自分の知る・知らないにかかわらず、一般解がある!と
考えて構わないでしょう。
それは、思考方法を「学」として学んできた算数や数学は、
常に、問題=課題に対しては、
回答に至る手続きを知る、あるいは暗記しておけば、
必ず、「答え」にたどり着くわけです。
�二重構造の強さ
私が、二重構造というのは「回答」の世界観です。
デザイン教育では、まず「課題」を与えて、
デザイン回答をやらせます。
それは、デザイン思考のトレーニングとして、
このデザイン解では、あれが足らないとか、
機能性を果たしていないとか、さらに問題が発生する、
という訓練です。
つまり、「回答」として提示されたデザイン解には、
二重性があるという見抜き方が必要です。
二重性には、性能的には「強度」があります。
すなわち、デザインは「綺麗事」だというある意味では、
開き直りの強さこそ、「回答」としてのデザイン解、
その強さだとひとまず考えておきたいと思います。
Tags: Answer, Question, デザイン思考, デザイン教育, デザイン解, トレーニング, 一般解, 世界観, 二重構造, �二重構造の強さ, 問題, 回答, 強度, 思いつき, 数学, 方法, 暗記, 機能性, 答え, 算数, 結果判断, 綺麗事, 考察, 見抜き方, 観点, 訓練, 話題, 課題, 資本主義からの闘争
Posted in 016「デザインと答」, 資本主義から逃走せよ!
目次を見る
2月 2nd, 2010 Posted 9:44 PM
2月2日 友引 (戊寅)
数学という
絶対的な
論理構造を求められる分野、
それを学際的に応用し、
知性的な範疇から
感性的な領域に入り込もうとするならば、
カタストロフィー理論のような
アプローチが必然だと、
私は確信している。
『デザインの極道論』かぐわしい
目次を見る





