指矩＝差し金あるいは指金には人類の度量の歴史が見事です。
度量衡にいたるまでには衡だけの歴史性が加わります。
果たして人類はなぜ、長さを測ったのでしょうか？
ここから出発しなければなりませんが、
単純には税収制度に他なりません。
そして、長さの単位は音でした。
だから笛の長さがある単位を決定していたと言われます。
今やレーザー光線で長さが決定されているから、
結局は同じ事＝音波＝波長、そして長さの単位がありました。
日本には、規矩術という優れた大工仕事の曲尺使い勝手がありました。
今やそのことは教えられてもいません。
私は宮大工の棟梁だった祖父に教わった経験があります。
指金というのは、
それこそ目の指金が＝メガネかもという推測もあるくらいです。
「念佛さし」という物差しがありました。
京都の竹は念仏をいつも聞いて育った竹ゆえに、
その竹で作られた物差しのことです。
この言葉を探り当てたのは故・桂米朝でした。
上方落語の｢天狗さし」のオチに登場する物差し屋のことです。
美大時代には、常にステンレス製のスケール尺を使っていました。
計測用だけではなくて、カッター切断のスケールとしてでした。
このスケール尺の裏には
デザイン用のマスキングテープを貼っていました。滑り止めでした。
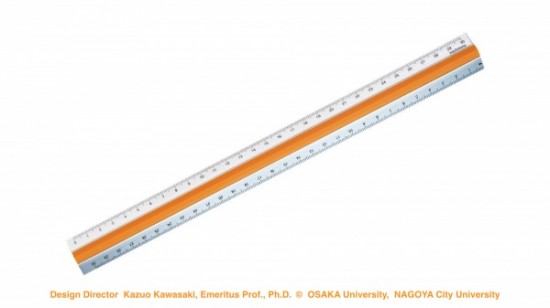
この物差しは、透明アクリルとステンレス、
そしてエラストマーの組み合わせです。
ようやく、滑り止めを施し、線引きもカッター使いも
こうした素材の組み合わせで作られた物差しです。
「ピタットルーラー」という商品名ですが、
今年度の日本文具大賞・機能部門賞にふさわしい製品として、
ここから新たな物差しが生まれると思っています。

私は教員という役目として、学生たちには、友人をつくることを
ことさら薦めて主張してきました。
ただし、友人というのは、今は亡き人たちに友人をつくることです。
彼ら、彼女らは、書籍の中に生きていますから、
本を読んで一方的に必死に友情をもてるぐらいになることを薦めます。
まして、その友人達の手稿があればそれは最高の友情だと考えます。
私の宝物は本物ではありませんが、ダヴィンチとクレーの手稿、
この二つは最高の物であり、おそらく再版されない限り、
美術館での特別展以外は見ることができません。
ダヴィンチはデッサン手稿でとても大きいのですが、
パウル・クレーの「造形理論ノート」は、彼の講義準備ノートです。
手稿ゆえに言葉は独語で書かれていますが、
出版物（今はもう手に入らない）では、ノートと翻訳があり、
ノートにはいわゆる図形、形態の彼なりの原則解釈があります。
おそらく、パウル・クレーほど厳密に図形、その造形解釈、
その論理化を熟考し言葉に置き換えて残してくれた人物はいません。
したがって、よく質問をしてくる学生には、
パウル・クレーと友情を持つことを吹聴してきたものです。
その実、今でも私がすべてを理解しているわけではありませんが、
時に、この造形表現はなにかおかしいと直感すると、
その説明は、彼の造形思考ノートで正解を確認することができます。
たとえば、単純なこと、矢印図形一つでも、なぜ、その平面性や
力学的な特性は、彼の言葉、文章で理解可能になります。
日本ではほとんどバウハウスの教育論が無視されていますが、
文理学際化の源、その教育原理はバウハウスにあります。
「教育原理」という教員資格単位がありましたが、
私は4年間この授業を受けましたが、単位を取らずなので、
結局、中高の美術科教員資格は持てませんでした。
理由は明快です。パウル・クレーの言説論無き「教育原理」などは、
大間違いだと今も思っているからです。
造形理論ノートには、造形課題とその教育理由が書かれています。

航海することと航空することには特別な単位があります。
一時間に一海里を進む速度のことです。
一海里は1852メートルですから、
それを1ノットの速度と呼びます。
私は、単純に1ノットは時速2km/h程度というイメージです。
そしてこの海里は地図では海図が用いられますから、
私は戦艦大和の最高速度が27ノットだから、
あの当時最大の大きさで時速は50km/hだったというイメージです。
したがって、審査会では常に高速性を求めていることには、
ハッとすることが多いのです。
航海とは、速度を求めるのではなくて、
航海する余裕の時間が重要だということです。
しかし、経済性を考えれば、速度性は技術開発の要点になります。
私が審査委員になって､初めて女性がプレゼンターでした。
正直、プレゼンはとても好感が持てるものでした。
ひょっとすれば女性がプレゼンすれば印象は良いのかも・・・
ところが、この審査会は実に詳細な質問があります。
それでも今年のグランプリは、この大型輸送船「双洋」です。
船には「喫水」という船舶と海面のインターフェイスがあります。
この船はその喫水を求めて、
ペンギンの泳ぎ方を参考にしたということです。
つまり、ペンギンは水滴で泳ぐように、
この船底に水泡を掃気するというわけです。
この開発はこれまでにもありました。
いきなり、船底に海水があるのではなくて、
水泡を掃気して高速性を求めようということでした。
結果、
省エネ効果があるという空気循環効果の最大化を求めたのです。
私はペンギンの泳法には水泡とペンギンの破毛効果だと思います。
それでも、船底での気泡流の最適化は、
大型貨物船の速度という経済性は審査委員全員が賛同しました。
これからの日本の造船開発、
その方向を提案したものとしてグランプリ船舶になりました。

「次元」に興味
デザインは意匠図という製図作成をします。
製図は、画法幾何学という領域から図法幾何学とか立体図学として、
もう300年の歴史的な蓄積があります。
しかし、その製図作成はデザイン技法として、
デザイナーにとっては、ほとんど無意識になるほど身体化してしまいます。
ところが、この無意識さを一度消却させてくれたのが、
私はCAD=Computer Aided Design (Drafting) だったと思っています。
つまり、三次元、いわゆる立体を二次元に描き出す技能法です。
ここで、私は「次元」に興味を持ちました。
とりあえず、基本的な次元をまとめておきます。
数学的な次元
■　数学的な次元
点を0次元・線を1次元・面を2次元・立体を3次元。
さらに、ここから点集合をどのように考察していくかが、
帰納法的に積み重ねられてきた空間系が、実数論的な解釈や、
現象空間との対比が生まれてきました。
こうした数学的な次元を、製図技法やスケッチでは行き着けないということが、
私のデザインから次元を見つめる一つの視点になっています。
物理的な次元
■　物理的な次元
ある量を決定するときに、数量性を表すのに適当な単位の設定から次元を決めていき、
その解析にまで至るということです。
たとえば、速さは長さに対して1次元、時間について-1次元、質量については０次元の量であり、
二つの量の積や加減で、関係＝構造をみるもう一つの視点です。
しかし、デザインにとっては、物理的な次元考察は、エンジニア任せにしています。
これは、素材開発をしていく時には、密度とか粘性とかをデザインアイディアで提案するときには、アイディアにデザイン価値を付加することができると、私は考えています。
現在、すでに日本のプラスティック成型が産業的に立ち後れているのは、
デザイナーが物理的な次元への提案ができていないことに起因していると判断しています。
多次元性への造形思考
そして、多次元性へのデザイン思考、造形思考は、
かってパウルクレーやカンデンスキーが予測していたことに重なっていると私は考えています。